【統計ソフト】[統計の基礎7]線形回帰(単回帰・重回帰)

統計ソフトを使う上で知っておくと役に立つ統計の基礎的な用語を紹介するシリーズです。
以下のリンクから関連のブログ記事を一覧できます。

・統計の基礎

今回は，線形回帰(単回帰・重回帰)についてです。

線形回帰，とは，回帰分析の手法の一つで，変数間の関係を線形(直線)で表現(予測)する分析方法です。

予測したい対象の変数(y)のことを，「目的変数(従属変数・応答変数)」などと呼びます。
目的変数の説明に用いる変数(x)のことを，「説明変数(独立変数・予測変数)」などと呼びます。

一般的に，目的変数にも説明変数にも量的な変数を用いますが，カテゴリカルな説明変数を0/1でダミー化して適用することもあります。

説明変数が1つであれば「単回帰」，

複数(n個)あれば「重回帰」となります。

説明に用いる説明変数以外の定数(α)を「切片」，
単回帰の時の説明変数の係数(β)のことを「傾き」と呼びます。

単回帰・重回帰は以下のような式で表現されます。

・単回帰

・重回帰

回帰式の予測の良さ(当てはまりの良さ)を表す数値のことを「決定係数」といい，記号では一般に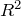と表現されます。決定係数は，0から1までの値をとり，1に近いほど、その回帰式の予測が良いことを表します。

決定係数は，説明変数の数が増えると高くなります。このため，説明変数が複数ある場合は，その数に応じて値を調整したものを「(自由度)調整済決定係数」と言います。重回帰モデルの比較の際などに使われます。

また，

説明変数の間に相関関係がある状態を，「(多重)共線性」がある，といいます。

重回帰分析は説明変数が互いに独立であることを前提としているため，共線性がある場合，回帰係数の推定が不安定になってしまいます。このため，重回帰分析では結果を見る際に，共線性についても確認する必要があります。

【統計ソフトヘルプデスク】
HP：https://www.mnc.toho-u.ac.jp/mc/mnc_stat.php
メール：mnc_stat☆ml.toho-u.jp
　※「☆」記号を「@」に置き換えて下さい。