統計ソフトを使う上で知っておくと役に立つ統計の基礎的な用語を紹介するシリーズです。
以下のリンクから関連のブログ記事を一覧できます。
以下のリンクから関連のブログ記事を一覧できます。
今回は,基本統計量についてです。
「統計量」とは,データの特徴や性質を表す数値のことで,代表的なものには次に上げるようなものがあります。これらの代表的・基本的な統計量のことを「基本統計量」と呼びます。
1. 量的な要約に基づく基本統計量
・平均(mean)
量的な変数の観測値を合計し,観測値の数で割ったものが「(算術)平均」です。全観測値の重心に位置します。分布が左右対称である場合は,ほぼ中心になりますが,分布が左右対称でない場合は,中心としての意味は弱くなります。その場合,平均の代わりにデータを代表する値として,中央値や最頻値が用いられることがあります(後述・下図も参照)。
データの中に,極端に大きな(小さな)値が含まれる場合,それに引きづられて値が大きく変動してしまうという特徴があります。
・分散(variance)
各観測値の平均からの差(偏差:deviation)を2乗して,その平均をとったものが「分散」です。2乗するため,平均との差の正負に関係なく計算できます。データの散らばり具合を表す指標の一つです。
・標準偏差(standard deviation, SD)
分散の正の平方根が「標準偏差」です。分散は2乗されているため,元の観測値と単位が合わなくなります。そこで,観測値と単位が同じになるように,平方根をとっています。データの散らばり具合を表す指標の一つです。
2. 順位に基づく基本統計量
・中央値(median)
観測値を小さい順に並べたときに,ちょうど真ん中に位置する観測値です。データの数が偶数の場合は,真ん中に位置する2つの値の平均が中央値となります。データの分布が左右対称から大きくズレているような場合,平均の代わりに用いられることがあります。
データの中に,極端に大きな(小さな)値が含まれている場合でも,平均に比べると影響が少ないという特徴があります。
・範囲(range)
観測値の最大値から最小値を引いたものです。データが分布している範囲を表します。
・四分位数(quartile)
観測値を小さい順に並べてデータ数を4等分した時の,区切りの位置にあたる値です。下から順に,それぞれ,第1四分位数(25%点),第2四分位数(50%点),第3四分位数(75%点)といいます。第2四分位数=中央値です。第3四分位数から第1四分位数を引いたものを,「四分位範囲」といいます。
3. 度数に基づく基本統計量
・最頻値(mode)
データをその値などに基づいて階級分けした場合に,最も多くの観測値が観測された階級値のことです。データの分布が左右対称から大きくズレているような場合,平均の代わりに用いられることがあります。なお,分布に山が2つ以上あるときに用いることは適切ではありません。
4. 平均・中央値・最頻値の関係
データの分布が左右対称かどうかで,平均・中央値・最頻値のデータの中での位置関係が変わってきます。
下図1のように,左右対称で中央に山がある分布の場合,これら3つの値はほぼ同じになります。
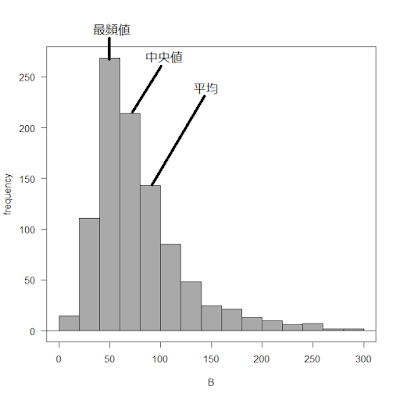
分布が左右対称から大きくずれるような場合は,これら3つの値は異なります。例えば下図2のように,右に歪んだ分布の場合,最頻値<中央値<平均,となります。
【統計ソフトヘルプデスク】
メール:mnc_stat☆ml.toho-u.jp
※「☆」記号を「@」に置き換えて下さい。